Metropolis Acceptance Criteria¶
Monte Carlo moves implemented in Cassandra preserve detailed balance between each pair of microstates \(m\) and \(n\)
where \(\Pi_{mn}\) is the probability of accepting the move from microstate \(m\) to microstate \(n\), \(\alpha_{mn}\) is the probability of attempting the move that will form \(n\) from \(m\), and \(p_m\) is the probability of \(m\) in the ensemble of interest.
In Cassandra, detailed balance is enforced via the Metropolis criterion
The ratio in Eq. (2) will often involve an exponential, e.g. \(e^{-\beta \Delta U}\). To preserve precision in the energy calculation, the acceptance probability is computed
The logarithm, defined in code as ln_pacc, is tested in the function
accept_or_reject() which is defined in file accept_or_reject.f90.
If ln_pacc is greater than 0 and less than a maximum numerical value,
\(\Pi_{mn}\) is computed and compared to a random number.
accept_or_reject = .FALSE.
IF (ln_pacc <= 0.0_DP) THEN
accept_or_reject = .TRUE.
ELSE IF ( ln_pacc < max_kBT) THEN
pacc = DEXP(-ln_pacc)
IF ( rranf() <= pacc ) THEN
accept_or_reject = .TRUE.
END IF
END IF
Ensembles¶
Canonical Monte Carlo¶
In the canonical ensemble, the number of molecules \(N\), the volume \(V\) and temperature \(T\) are all constant. The position, orientation and conformation of a semi-flexible molecule with fixed bond-lengths containing \(M\) atoms is given by a \(2M+1\)-dimensional vector \(\mathbf{q}\). The positions, orientations and conformations of all \(N\) molecules are denoted \(\mathbf{q}^N\).
The probability of observing microstate \(m\) with configuration \(\mathbf{q}_m^N\) is
where \(\beta\) is the inverse temperature \(1/k_BT\), \(U\) is the potential energy, the differential volume \(d\mathbf{q}^N\) is included to make \(p_m\) dimensionless and \(Z\) is the configurational partition function
The integral is over all \(N(2M+1)\) degrees of freedom. The ratio of microstate probabilities follows from Eq. (4)
The configurational partition function \(Z\) and differential volume \(d\mathbf{q}^N\) both cancel, leaving only the ratio of Boltzmann factors.
New configurations are generated by attempting moves that translate, rotate and regrow a randomly selected molecule. For more information on the acceptance rules of these moves, please refer to Molecule Translation, Molecule Rotation and Molecule Regrowth, respectively.
Above, the microstate probability is normalized by the configurational partition function \(Z\) because the only relevant degrees of freedom are configurational. In other ensembles, the full canonical partition function \(Q\) appears, integrated over both configuration space \(\mathbf{q}^N\) and momenta space \(\mathbf{p}_q^N\)
where the 2\(M\)+1 momenta \(\mathbf{p}_q\) are conjugate to the generalized coordinates \(\mathbf{q}\). The momenta and configuration integrals are separable, and the single molecule momenta integrals are all identical.
where \(Q(1,V,T)\) is the partition function of a single molecule in a box. The center of mass integrals for a single molecule are separable from the integrals over rotational and internal degrees of freedom:
where \(\Lambda\) is the de Broglie wavelength of the molecule and the rotational and internal momenta integrals in \(Q_{rot+int}\) are not separable since the moments of inertia will depend on the conformation adopted by the molecule. The configurational partition function is further separable into center of mass (translational), orientational and internal degrees of freedom:
where the volume \(V\) is the translational partition function and \(Z_{rot}\) equals \(4\pi\) for a linear molecule and \(8\pi^2\) for a nonlinear molecule.
Isothermal-Isobaric Monte Carlo¶
In the isothermal-isobaric ensemble, the number of particles \(N\), the pressure \(P\) and temperature \(T\) are all constant while the volume \(V\) and energy \(E\) fluctuate. The partition function is
where \(Q\) is dimensionless and \(\Delta\) has dimensions of volume. The kinetic contribution to \(\Delta\) is independent of the pressure or volume and consequently separable from the configurational contribution, \(\Delta_Z\)
The probability of the system having volume \(V\) is
The probability of observing microstate \(m\) with configuration \(\mathbf{q}_m^N\) and volume \(V_m\) is
where the differential element \(d\mathbf{q}_m^N\) has subscript \(m\) becuase it scales with the volume \(V_m\). The ratio of microstate probabilities is
New configurations are generated via Molecule Translation, Molecule Rotation and Molecule Regrowth, and Volume Scaling.
Grand Canonical Monte Carlo¶
In the grand canonical ensemble, the chemical potential \(\mu\), the volume \(V\) and temperature \(T\) are held constant while the number of molecules \(N\) and energy \(E\) fluctuate. The partition function is
The probability of the system having \(N\) molecules is
The probability of observing microstate \(m\) with \(N_m\) molecules and configuration \(\mathbf{q}_m^{N_m}\) is
Note that Eq. (17) does not contain the factorial \(N_m!\) that accounts for indistinguishable particles. In a simulation, particles are distinguishable: they are numbered and specific particles are picked for MC moves. The ratio of microstate probabilities is
Alternatively, Eq. (18) can be recast to use the fugacity \(f\) instead of the chemical potential \(\mu\). The relationship between \(\mu\) and \(f\) is
Inserting Eq. (19) into Eq. (18) yields
Fluctuations in the number of molecules are achieved by inserting and deleting molecules. A successful insertion increases the number of molecules from \(N\) to \(N\) + 1, i.e. \(\Delta N = 1\). A successful deletion decreases the number of molecules from \(N\) to \(N\) - 1, i.e. \(\Delta N = -1\).
Random insertions and deletions (see Inserting a Molecule Randomly and Deleting a Molecule Inserted Randomly) in the liquid phase typically have very large \(\Delta U\) due to core overlap and dangling bonds, respectively, making the probability of acceptance very low. To overcome this challenge, insertions in Cassandra are attempted using Configurational Bias Monte Carlo. See Inserting a Molecule with Configurational Bias Monte Carlo and Deleting a Molecule that was Inserted via Configurational Bias Monte Carlo for details.
Gibbs Ensemble Monte Carlo¶
The Gibbs Ensemble Monte Carlo method is a standard technique for studying phase equilibria of pure fluids and mixtures. It is often used to study vapor-liquid equilibria due to its intuitive physical basis. In Cassandra, the NVT and NPT versions of the Gibbs Ensemble (GEMC-NVT and GEMC-NPT) are implemented. The GEMC-NVT method is suitable for simulating vapor liquid equilibria of pure systems, since pure substances require the specification of only one intensive variable (temperature) to completely specify a state of two phases. By contrast, mixtures require the specification of an additional degree of freedom (pressure). Thus, in the GEMC-NPT method, the pressure is specified in addition to temperature.
The partition functions and microstate probabilities are derived for Gibbs Ensemble-NVT and Gibbs Ensemble-NPT, below. In both cases, thermal equilibrium is attained by performing translation, rotation and regrowth moves. The acceptance rules for these moves are identical to those presented in Molecule Translation, Molecule Rotation, Molecule Regrowth and Regrowing a Molecule with Configurational Bias Monte Carlo. Pressure equilibrium is achieved by exchanging volume in the case of GEMC-NVT, or independently changing the volume of each box in the case of GEMC-NPT. The acceptance rule for the exchanging volume in GEMC-NVT is derived and its Cassandra implementation is presented in Volume Exchange Moves. The acceptance rule for swapping a molecule in either GEMC-NVT or GEMC-NPT are derived in Molecule Exchange Moves.
Gibbs Ensemble-NVT¶
In the GEMC-NVT method, there are two boxes A and B. To achieve phase equilibrium, the boxes are allowed to exchange volume and particles under the constraint of constant total volume (\(V^t=V^A + V^B\)) and constant number of particles (\(N^t=N^A + N^B\)). The partition function is
where \(Q(N,V,T)\) is the canonical partition function given in Eq. (7). Since both boxes are maintained at the same temperature the kinetic contribution of each molecule is independent of the box in which it is located. The configurational partition function \(Z_{GE}\) is defined by separating the momenta integrals from the configurational integrals, volume integrals and molecular sums
The probability of microstate \(m\) in the NVT Gibbs ensemble is
Note that the molecule number factorials are not included in Eq. (23), as particles are distinguishable in a simulation (see also Eq. (17)).
For two microstates \(m\) and \(n\) that differ only by a thermal move of a molecule in box A, the ratio of microstate probabilities is
similar to Eq. (6). As a result, thermal moves have the same acceptance rule in GEMC-NVT as they do in other ensembles. The differential elements \(d\mathbf{q}\) will likewise cancel from the acceptance criteria when swapping a molecule between boxes. When exchanging volume, however, the differential elements will reduce to a ratio of the old volume to the new, as shown in Volume Exchange Moves.
Gibbs Ensemble-NPT¶
The GEMC-NPT method is only valid for sampling phase equilibria in multicomponent systems. It is similar to GEMC-NVT, except that the volume of each box fluctuates independently. Consequently, the total volume of the system is not constant and the pressure must be specified in addition to the temperature. This is consistent with the Gibbs phase rule for mixtures, which requires the specification of two intensive variables (e.g. pressure and temperature) to fully specify a state with two phases.
The partition function is
where \(\{N\}\) is the number of molecules of each species, \(\Delta({N},P,T)\) is the multicomponent analog to Eq. (10), and there is a separate sum for each species over the number of molecules in box A. The kinetic contribution to \(\Delta_{GE}\) can be separated giving the configurational partition function
where \(\Delta_Z({N},P,T)\) is the multicomponent analog to Eq. (11). The probability of microstate \(m\) in this ensemble is
Similar to GEMC-NVT, the ratio of probabilities between microstates that differ by only a thermal move in box A is
Volume changes are only attempted on one box at a time. The ratio of probabilities between microstates that differ only by the volume of box A is
similar to Eq. (14). As a result, volume moves in GEMC-NPT have the same acceptance criteria as in the NPT ensemble (see Eq. (31)).
Monte Carlo Moves¶
Molecule Translation¶
A molecule is translated by moving its center of mass in each Cartesian direction by a random amount chosen from the uniform distribution on the interval [-\(\delta r_{max},\delta r_{max}\)]. The maximum displacement \(\delta r_{max}\) must be given in the input file. The translation move is symmetric in forward and reverse directions. That is, either microstate \(n\) can be formed from microstate \(m\) and vice versa by moving one molecule within \(\delta r_{max}\) in each Cartesian direction, or microstate \(n\) cannot be formed at all. As a result, \(\alpha_{mn} = \alpha_{nm}\).
The acceptance probability for a translation move follows from Eq. (6)
In Cassandra, the translation move is implemented in the subroutine
Translate defined in move_translate.f90. The variable names in the move_translate.f90 code
are identified with the symbols from
Eq. (28) in Table 8
ln_pacc = beta(ibox) * delta_e
accept = accept_or_reject(ln_pacc)
| Symbol | Code name |
|---|---|
| \(\beta\) | beta(this_box) |
| \(\Delta U\) | delta_e |
Molecule Rotation¶
A linear molecule is rotated differently than a nonlinear molecule. A molecule is identified as linear if it is composed of 2 atoms or if all the angles are rigid with a bond angle of 180\(^{\circ}\).
If the molecule is linear:
- Pick three random angles: \(\phi\) on [\(-\pi,\pi\)], \(\cos(\theta)\) on [-1,1], and \(\psi\) on [\(-\pi,\pi\)].
- With the origin at the molecule’s center of mass, rotate by \(\phi\) around \(z\), rotate by \(\theta\) around \(x'\), and rotate by \(\psi\) around \(z'\), as shown below.

Fig. 2 Procedure for rotating linear molecules. Image from mathworld.wolfram.com/EulerAngles.html.
Even though three angles are randomly chosen, the probability of the resulting orientation is \(d\cos(\theta)d\phi/4\pi\).
If the molecule is nonlinear:
- Randomly select an axis: \(x\), \(y\), or \(z\).
- Choose a random angular displacement \(\delta \theta\) from \([-\delta \theta_{max}, \delta \theta_{max}]\). \(\delta \theta_{max}\) must be given in the input file.
- Rotate the molecule around a vector parallel to the selected axis and through its center of mass by \(\delta \theta\).
In either case, the rotation move is symmetric, \(\alpha_{mn} =
\alpha_{nm}\), and the acceptance criteria is given by Eq. (28). The
rotation move is implemented in subroutine Rotate defined in
move_rotate.f90.
ln_pacc = beta(ibox) * delta_e
accept = accept_or_reject(ln_pacc)
Molecule Regrowth¶
Internal degrees of freedom in flexible molecules are sampled by deleting one or more fragments from the molecule and replacing the deleted fragments with conformations from a reservoir of fragment conformations. If the molecule consists of only a single fragment (e.g, water, all atom methane, united atom propane, all atom cyclohexane), the entire molecule is deleted and replaced as follows:
- Randomly select a molecule \(i\) with uniform probability \(1/N\), record its center-of-mass position and delete it.
- Select a molecular conformation with Boltzmann probability \(e^{-\beta U(\mathbf{q}_{int,n}^{(i)})}/Z_{int}\), where \(\mathbf{q}_{int,n}^{(i)}\) are the internal bond or improper angles of molecule \(i\) in microstate \(n\) and \(Z_{int}\) is the configurational partition function over internal degrees of freedom (see Eq. (9)).
- Pick three random angles: \(\phi\) on [\(-\pi,\pi\)],
\(\cos(\theta)\) on [-1,1], and \(\psi\) on [\(-\pi,\pi\)].
Rotate the molecule as shown in
fig:euler_angles. The probability of the resulting orientation is \(d\mathbf{q}_{rot}/Z_{rot}\), which for a nonlinear molecule is \(d\cos(\theta) d\phi d\psi / 8 \pi^2\). - Place the molecule with the selected conformation and orientation at the same center-of-mass position as the deleted molecule.
Regrowing a monoatomic particle has no effect. Regrowing a linear molecule is the same as rotating it. The overall probability \(\alpha_{mn}\) of regrowing a molecule with the selected orientation and conformation is
where \(\mathbf{q}_n^{(i)}\) denotes the position, orientation and conformation of molecule \(i\) in microstate \(n\) and \(U(\mathbf{q}_n^{(i)})\) is the potential energy of the isolated molecule \(i\), i.e. the intramolecular potential energy. The reverse probability \(\alpha_{nm}\) is identical except for the intramolecular potential energy \(U(\mathbf{q}_m^{(i)})\) of molecule \(i\) in microstate \(m\). Using Eqs. (6) and (29), the acceptance criteria for the regrowth of a single fragment molecule is
Only the change in the intermolecular potential energy between molecule \(i\) and the other \(N-1\) molecules contributes to the acceptance criteria. The code that implements Eq. (30) is shown in code in Regrowing a Molecule with Configurational Bias Monte Carlo
If the molecule consists of more than one fragment (e.g., all atom ethane, all atom toluene, united atom butane), a bond is cut and the severed fragments are regrown using Configurational Bias Monte Carlo (CBMC). See Regrowing a Molecule with Configurational Bias Monte Carlo for more details.
Volume Scaling¶
In Cassandra, new volumes are sampled as follows:
- Pick a random volume \(\Delta V\) with uniform probability from the interval [\(-\delta V_{max}\), \(\delta V_{max}\)]. The trial volume is \(V + \Delta V\).
- Scale the box lengths uniformly.
- Scale the center of mass of each molecule uniformly.
The probability of selecting \(\Delta V\) is the same as selecting \(-\Delta V\) which makes scaling the volume symmetric, \(\alpha_{mn}=\alpha_{nm}\). Scaling the configurations changes the differential element \(d\mathbf{q}_m^N\) surrounding configuration \(\mathbf{q}_m^N\). Only the molecular centers of mass change, so we can separate \(d\mathbf{q}\) into 3 center of mass coordinates \(d\mathbf{r}_{com}\) and 2\(M\)-2 orientational and internal coordinates \(d\mathbf{q}_{rot+int}\). The scaled center of mass positions are held constant, making \(d\mathbf{r}_{com} = V d\mathbf{s}_{com}\). The acceptance probability for a volume scaling move is
The volume scaling move is implemented in subroutine Volume_Change defined in move_volume.f90.
ln_pacc = beta(this_box) * delta_e &
+ beta(this_box) * pressure(this_box) * delta_volume &
- total_molecules * DLOG(box_list(this_box)%volume/box_list_old%volume)
accept = accept_or_reject(ln_pacc)
| Symbol | Code name |
|---|---|
| \(\beta\) | beta(this_box) |
| \(\Delta U\) | delta_e |
| \(P\) | pressure(this_box) |
| \(\Delta V\) | delta_volume |
| \(N\) | total_molecules |
| \(V_n\) | box_list(this_box)%volume |
| \(V_m\) | box_list_old%volume |
Inserting a Molecule with Configurational Bias Monte Carlo¶
In Configurational Bias Monte Carlo (CBMC), the molecular conformation of the inserted molecule is molded to the insertion cavity. First, the molecule is parsed into fragments such that each fragment is composed of (a) a central atom and the atoms directly bonded to it (see Fig. 3), or (b) a ring of atoms and all the atoms directly bonded to them. Then, a position, orientation and molecular conformation of the molecule to be inserted are selected via the following steps:
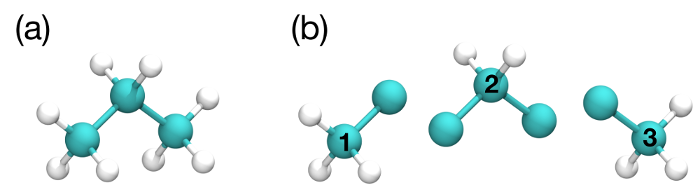
Fig. 3 (a) An all-atom model of propane. (b) The same model as in (a), but parsed into three fragments.
- Select the order in which each fragment of the (\(N+1\))th molecule will
be placed. The probability of the resulting sequence is \(p_{seq}\). (See
example in Table 10)
- The first fragment \(i\) is chosen with uniform probability 1/\(N_{frag}\).
- Subsequent fragments must be connected to a previously chosen fragment and are chosen with the uniform probability 1/\(N_{cnxn}\), where the number of connections \(N_{cnxn}= \sum_{ij}{\delta_{ij} h_{i} (1-h_{j})}\) is summed over all fragments \(i\) and \(j\). \(h_i\) is 1 if fragment \(i\) has been previously chosen and 0 otherwise. \(\delta_{ij}\) is 1 if fragments \(i\) and \(j\) are connected and 0 otherwise.
- Select a conformation for fragment \(i\) with Boltzmann probability \(e^{-\beta U(\mathbf{q}_{frag_i})}d\mathbf{q}_{frag_i}/Z_{frag_i}\), where \(\mathbf{q}_{frag_i}\) are the internal degrees of freedom (angles and/or impropers) associated with fragment \(i\).
- Select an orientation with uniform probability \(d\mathbf{q}_{rot}/Z_{rot}\).
- Select a coordinate for the center of mass (COM) of fragment \(i\):
- Select \(\kappa_{ins}\) trial coordinates \(\mathbf{r}_k\), each with uniform probability \(d\mathbf{r}/V\). Since one of the trial coordinates will be selected later, the individual probabilities are additive. The probability of the collection of trial coordinates is \(\kappa_{ins}d\mathbf{r}/V\).
- Compute the change in potential energy \(\Delta U_k^{ins}\) of inserting fragment \(i\) at each position \(\mathbf{r}_k\) into configuration \(\mathbf{q}_m^N\).
- Select one of the trial coordinates with probability \(e^{-\beta \Delta U_k^{ins}} / \sum_k{e^{-\beta \Delta U_k^{ins}}}\).
- For each additional fragment \(j\):
- Select a fragment conformation with Boltzmann probability\(e^{-\beta U(\mathbf{q}_{frag_j})}d\mathbf{q}_{frag_j}/Z_{frag_j}\)
- Select the first of \(\kappa_{dih}\) trial dihedrals \(\phi_0\) with uniform probability from the interval [0,:math:frac{2pi}{kappa_{dih}}). Additional trial dihedrals are equally spaced around the unit circle, \(\phi_k=\phi_{k-1}+2\pi/\kappa_{dih}\). The probability of selecting \(\phi_0\) is \(\kappa_{dih}d\phi/2\pi\).
- Compute the change in potential energy \(\Delta U_k^{dih}\) of attaching fragment \(j\) to the growing molecule with each dihedral \(\phi_k\).
- Select one of the trial dihedrals with probability \(e^{-\beta \Delta U_k^{dih}} / \sum_k{e^{-\beta \Delta U_k^{dih}}}\).
| Sequence | \(p_{seq}\) |
|---|---|
| 1 2 3 | 1/3 |
| 2 1 3 | 1/6 |
| 2 3 1 | 1/6 |
| 3 2 1 | 1/3 |
The overall probability \(\alpha_{mn}\) of attempting the insertion with the selected position, orientation and conformation is
where \(Z_{frag} = \prod_i Z_{frag_i}\) is the configurational partition function over degrees of freedom internal to each fragment, \(U(\mathbf{q}_{frag}) = \sum_iU(\mathbf{q}_{frag_i})\) is the summed potential energy of each of the (disconnected) fragments, \(\Omega_{dih} = (2\pi)^{N_{frag}-1}\) and \(p_{bias}\) is
Note that the term \(VZ_{rot}Z_{frag}\Omega_{dih}\) in the denominator of Eq. (32) differs from \(Z(1,V,T)=VZ_{rot}Z_{int}\).
In the reverse move, 1 of the \(N+1\) particles is randomly selected for deletion. The probability \(\alpha_{nm}\) of picking the molecule we just inserted is
Combining Eqs. (32) and (34) with Eq. (18) or Eq. (20) gives the acceptance probability for a CBMC insertion move
where \(\mu'\) and \(f'\) are, respectively, a shifted chemical potential and a skewed fugacity,
All of the terms in Eqs. (60) and (38) are intensive. GCMC simulations using Eqs. (35) and (36) will converge to the same average density regardless of the simulation volume \(V\). However, the values of \(\mu'\) or \(f'\) that correspond to the converged density will not match tabulated values of \(\mu\) or \(f\) computed from experimental data.
Note that the term \(Z^{IG}/\Omega\) from Macedonia *et al* would be equivalent to \(Z_{int}/\Omega_{frag}\Omega_{dih}\) in the nomenclature used here. The configurational partition function of the disconnected fragments integrates over a Boltzmann factor, \(Z_{frag} = \int e^{-\beta U(\mathbf{q}_{frag})} d\mathbf{q}_{frag}\), whereas the term \(\Omega_{frag} = \int d\mathbf{q}_{frag}\) does not.
In Cassandra, the insertion move is implemented in the subroutine Insertion in move_insert.f90. The relevant lines from version 1.2 are quoted below. The variable names in the move_insert.f90 code are identified with symbols in Table 11.
! change in energy less energy used to bias selection of fragments
dE_frag = E_angle + nrg_ring_frag_tot
ln_pacc = beta(ibox) * (dE - dE_frag)
! chemical potential
ln_pacc = ln_pacc - species_list(is)%chem_potential * beta(ibox)
! bias from CBMC
ln_pacc = ln_pacc + ln_pbias
! density
ln_pacc = ln_pacc + DLOG(REAL(nmols(is,ibox),DP)) &
+ 3.0_DP*DLOG(species_list(is)%de_broglie(ibox)) &
- DLOG(box_list(ibox)%volume)
accept = accept_or_reject(ln_pacc)
Note that GCMC simulations using fugacities are currently not supported in Cassandra. This feature will be implemented in a future release.
| Symbol | Code name |
|---|---|
| \(\beta\) | beta(ibox) |
| \(\Delta U\) | dE |
| \(U(\mathbf{q}_{frag})\) | dE_frag |
| ln(\(p_{seq}p_{bias})\) | ln_pbias |
| \(\mu'\) | species_list(is)%chem_potential |
| \(N\) | nmols(is,this_box) |
| \(V\) | box_list(this_box)%volume |
| \(\Lambda\) | species_list(is)%de_broglie(this_box) |
Deleting a Molecule that was Inserted via Configurational Bias Monte Carlo¶
The probability \(\alpha_{mn}\) of choosing a molecule to delete is
The probability of the reverse move \(\alpha_{nm}\) requires knowledge of the sequence and biasing probabilities \(p_{seq}\) and \(p_{bias}\) that would have been used to place the molecule if it was being inserted. \(p_{seq}\) and \(p_{bias}\) can be calculated using the following procedure:
- Select the fragment order using the same procedure for inserting a molecule. The probability of the resulting sequence is \(p_{seq}\).
- The first fragment in the sequence is fragment \(j\). Calculate the intramolecular potential energy of fragment \(j\)’s current conformation, \(U(\mathbf{q}_{frag_j})\). The probability of this conformation is Boltzmann \(e^{-\beta U(\mathbf{q}_{frag_j})}d\mathbf{q}_{frag_j}/Z_{frag_j}\).
- The probability of the fragment’s current orientation is \(d\mathbf{q}_{rot}/Z_{rot}\).
- Calculate the weight of the fragment’s current center of mass (COM)
coordinates:
- Compute the interaction potential energy \(\Delta U^{ins}\) between fragment \(j\) and the other \(N-1\) molecules.
- Select \(\kappa_{ins}-1\) trial coordinates \(\mathbf{r}_k\), each with uniform probability \(d\mathbf{r}/V\).
- Calculate the weight of the fragment’s current COM amongst the trial coordinates, \(e^{-\beta \Delta U^{ins}} / \sum_k{e^{-\beta \Delta U_k^{ins}}}\).
- For each additional fragment \(j\):
- Calculate the intramolecular potential energy of fragment \(j\)’s current conformation, \(U(\mathbf{q}_{frag_j})\). The weight of this conformation in the Boltzmann distribution is \(e^{-\beta U(\mathbf{q}_{frag_j})}d\mathbf{q}_{frag_j}/Z_{frag_j}\).
- Calculate the interaction potential energy \(\Delta U^{dih}\) between fragment \(j\), on the one hand, and fragments \(i\) through \(j-1\) and the other \(N-1\) molecules.
- Calculate the current dihedral \(\phi_0\) of fragment \(j\). Compute the interaction potential energy \(\Delta U_k^{dih}\) at \(\kappa_{dih}-1\) trial dihedrals \(\phi_k = \phi_{k-1} + 2\pi/\kappa_{dih}\).
- Compute the weight of \(\phi_0\) amongst the trial dihedrals, \(e^{-\beta \Delta U^{dih}}/ \sum_k{e^{-\beta \Delta U_k^{dih}}}\).
The overall probability \(\alpha_{nm}\) is
The acceptance criteria for deleting a molecule inserted via CBMC is
In Cassandra, the deletion move is implemented in the subroutine Deletion in move_delete.f90. The relevant lines are quoted below. The variable names in move_delete.f90 code are identified with symbols in Table 12.
! change in energy less energy used to bias fragment selection
dE_frag = - E_angle - nrg_ring_frag_tot
ln_pacc = beta(ibox) * (dE - dE_frag)
! chemical potential
ln_pacc = ln_pacc + beta(ibox) * species_list(is)%chem_potential
! CBMC bias probability
ln_pacc = ln_pacc - ln_pbias
! dimensionless density
ln_pacc = ln_pacc + DLOG(box_list(ibox)%volume) &
- DLOG(REAL(nmols(is,ibox),DP)) &
- 3.0_DP*DLOG(species_list(is)%de_broglie(ibox))
accept = accept_or_reject(ln_pacc)
Note that GCMC simulations using fugacities are currently not supported in Cassandra. This feature will be implemented in a future release.
| Symbol | Code name |
|---|---|
| \(\beta\) | beta(ibox) |
| \(\Delta U\) | dE |
| \(U(\mathbf{q}_{frag})\) | dE_frag |
| \(ln(p_{seq}p_{bias})\) | ln_pbias |
| \(\mu'\) | species_list(is)%chem_potential |
| \(N\) | nmols(is,this_box) |
| \(V\) | box_list(this_box)%volume |
| \(\Lambda\) | species_list(is)%de_broglie(this_box) |
Regrowing a Molecule with Configurational Bias Monte Carlo¶
Regrowing a molecule that has more than one fragment is a combination deletion and insertion move. Starting from microstate \(m\):
- Randomly select a molecule with uniform probability \(1/N\).
- Randomly select a bond to cut on the selected molecule with uniform probability \(1/N_{bonds}\).
- Delete the fragments on one side of the bond or the other with equal probability. The number of deleted fragments is \(N_{del}\).
- Reinsert the deleted fragments using the CBMC procedures for selecting the order of inserting the fragments, choosing a fragment conformation, and a connecting dihedral value (see Inserting a Molecule with Configurational Bias Monte Carlo).
The overall probability \(\alpha_{mn}\) of attempting to regrow the molecule with the selected conformation is
where \(Z_{del} = \prod_i Z_{frag_j}\) is the configurational partition function over degrees of freedom internal to the deleted fragments, \(U(\mathbf{q}^{(i)}_{del,n}) = \sum_jU(\mathbf{q}_{frag_j})\) is the summed potential energy of each deleted fragment with the conformations in microstate \(n\), \(\Omega_{del} = (2\pi)^{N_{del}}\) and \(p_{forward}\) is the biasing probability
The reverse move is identical except for the potential energy of the deleted fragments \(U(\mathbf{q}^{(i)}_{del,m})\) in microstate \(m\) and the biasing probability \(p_{reverse}\) which will depend on the values of the connecting dihedrals. Using Eqs. (6) and (41), the acceptance criteria is:
Eq. (42) is implemented in subroutine cut_N_grow() in file move_regrow.f90.
ln_pacc = beta(ibox) * (delta_e_n - nrg_ring_frag_forward) &
- beta(ibox) * (delta_e_o - nrg_ring_frag_reverse) &
+ ln_pfor - ln_prev
accept = accept_or_reject(ln_pacc)
| Symbol | Code name |
|---|---|
| \(\beta\) | beta(ibox) |
| \(U(\mathbf{q}^N_n) - U(\mathbf{q}^{(i)}_{del,n})\) | delta_e_n - nrg_ring_frag_forward |
| \(U(\mathbf{q}^N_m) - U(\mathbf{q}^{(i)}_{del,m})\) | delta_e_o - nrg_ring_frag_reverse |
| \(ln(p_{forward})\) | ln_pfor |
| \(ln(p_{reverse})\) | ln_prev |
Volume Exchange Moves¶
In GEMC-NVT, volume is exchanged between the two boxes to achieve pressure equilibrium using a symmetric volume move, \(\alpha_{mn} = \alpha_{nm}\). If box A is shrunk by \(\Delta V\), then box B grows by \(\Delta V\) and vice versa. \(\Delta V\) is chosen from a uniform distribution with probability \(1/\delta V_{max}\), where \(\delta V_{max}\) is an adjustable parameter. The scaled center of mass positions of each molecule are held constant, introducing a ratio of volumes into the acceptance criteria similar to Eq. (31).
The acceptance rule is derived from Eq. (23) and yields
| Symbol | Code name |
|---|---|
| \(\beta^A\) | beta(box1) |
| \(\beta^B\) | beta(box2) |
| \(\Delta U^A\) | delta_e_1 |
| \(\Delta U^B\) | delta_e_2 |
| \(N^A\) | tot_mol_box_1 |
| \(N^B\) | tot_mol_box_2 |
| \(V^A_m\) | box_list(box1)%volume |
| \(V^B_m\) | box_list(box2)%volume |
| \(V^A_n\) | box_list_old_1%volume |
| \(V^B_n\) | box_list_old_2%volume |
This acceptance rule is implemented in the file move_vol_swap.f90 as follows:
ln_pacc = beta(box_grw) * delta_e_1 + beta(box_shk) * delta_e_2 &
- REAL(SUM(nmols(:,box_grw)),DP) * DLOG( box_list(box_grw)%volume / box_list_old_1%volume) &
- REAL(SUM(nmols(:,box_shk)),DP) * DLOG( box_list(box_shk)%volume / box_list_old_2%volume)
Molecule Exchange Moves¶
In either GEMC-NVT or GEMC-NPT, molecules are swapped between the two boxes to equalize the chemical potential of each species. The ratio of probabilities for microstates that differ only by swapping a molecule of species \(s\) from box \(out\) to box \(in\) is
where the differential elements \(d\mathbf{q}\) will cancel from the acceptance criteria by similar terms in \(\alpha_{mn}/\alpha_{nm}\). The particle swap is not symmetric since each molecule is inserted and deleted using configurational bias. The forward probability \(\alpha_{mn}\) follows from the steps used to swap a molecule:
- Pick a box \(out\) with probability \(p_{box}\), where
\(p_{box}\) is
- the ratio of molecules in box, \(N^{out}/N^t\) (default)
- a fixed probability given in the input file
- If necessary, pick a species \(s\) with probability
\(p_{spec}\), where \(p_{spec}\) is
- the ratio of molecules of species \(s\) in box \(out\), \(N^{out}_s/N^{out}\) (default)
- a fixed probability given in the input file
- Pick a molecule of species \(s\) from the box \(out\) with uniform probability, \(1/N^{out}_s\)
- Insert molecule in box \(in\) using protocol presented in Inserting a Molecule with Configurational Bias Monte Carlo
If the default probabilities are used at each step, then a swap is attempted for each molecule with uniform probability
The attempt probability of generating configuration \(n\)
where \(p_{bias}\) is defined in Eq. (33). The reverse probability \(\alpha_{nm}\) is calculated similarly. The acceptance rule is
where \(p_{seq}\) does not appear since the same fragment regrowth sequence
is used in the forward and reverse moves. The molecule swap move is implemented
in the file move_mol_swap.f90 as follows:
| Symbol | Code name |
|---|---|
| \(\beta^A\) | beta(box_out) |
| \(\beta^B\) | beta(box_in) |
| \(\Delta U^A\) | -delta_e_out |
| \(\Delta U^B\) | delta_e_in |
| \(U^{in}(\mathbf{q}_{frag,n})\) | e_angle_in + nrg_ring_frag_in |
| \(U^{out}(\mathbf{q}_{frag,m})\) | e_angle_out + nrg_ring_frag_out |
| \(V^{out}\) | box_list(box_out)%volume |
| \(V^{in}\) | box_list(box_in)%volume |
| \(ln(p_{bias,n})\) | ln_pfor |
| \(ln(p_{bias,m})\) | ln_prev |
| \(p_{out,m} p_{spec,m}\) | P_forward |
| \(p_{out,n} p_{spec,n}\) | P_reverse |
delta_e_in_pacc = delta_e_in
delta_e_out_pacc = delta_e_out
delta_e_in_pacc = delta_e_in_pacc - e_angle_in - nrg_ring_frag_in
delta_e_out_pacc = delta_e_out_pacc - e_angle_out - nrg_ring_frag_out
ln_pacc = beta(box_in)*delta_e_in_pacc - beta(box_out)*delta_e_out_pacc
ln_pacc = ln_pacc - DLOG(box_list(box_in)%volume) &
+ DLOG(box_list(box_out)%volume) &
- DLOG(REAL(nmols(is,box_out),DP)) &
+ DLOG(REAL(nmols(is,box_in) + 1, DP))
ln_pacc = ln_pacc + ln_pfor - ln_prev &
+ DLOG(P_forward / P_reverse)
accept = accept_or_reject(ln_pacc)
Multicomponent Systems¶
Excluding Gibbs Ensemble-NPT, the acceptance rules for all the Monte Carlo techniques expressed in this chapter have been developed for pure component systems. The Monte Carlo moves and acceptance criteria for multicomponent systems are straightforward extensions of the pure component moves. The only modification needed to translate, rotate and regrow molecules is to first select a species. In these moves, a species is selected randomly in proportion to its mole fraction \(N_i/N\). When inserting and deleting a molecule, the mole fractions of each species change. In these cases, a species in a multicomponent system is selected instead with uniform probability \(1/N_{species}\). In either case, species selection is symmetric for both forward and reverse moves and so cancels from the acceptance criterion.
CBMC Widom Insertion Method¶
The Widom insertion method, also known as the test particle insertion method, can be used to calculate the shifted chemical potential of a species during a simulation. From shifted chemical potentials, excess chemical potentials and Henry’s constants can be calculated.
The chemical potential \(\mu\) of a given species \(a\) in the NVT ensemble is defined in Eq. (47), where \(F\) is the Helmholtz free energy.
For the sake of simpler notation, the following derivation is for a pure component system, but it can be easily extended to multicomponent systems.
The Helmholtz free energy is defined in Eq. (48).
Approximating Eq. (47) with the addition of a single molecule and substituting Eq. (48) yields Eq. (49).
Eq. (49) can be combined with Eq. (7) to obtain Eq. (50).
The configurational partition function \(Z(N,V,T)\) is defined in Eq. (51), which leads to (52), where \(\Delta U = U(\mathbf{q}^{N+1}) - U(\mathbf{q}^N)\) is the change in potential energy of inserting the molecule, \({\langle ... \rangle}_N\) denotes NVT ensemble averaging over configurational space of the system of \(N\) particles, and \(\mathbf{q}_{N+1}\) denotes the generalized coordinates of only the inserted molecule.
The final integral in Eq. (52) can be estimated by CBMC importance sampling with test molecules inserted as described in Inserting a Molecule with Configurational Bias Monte Carlo. This is demonstrated in Eq. (53), where \(n_{IPC}\) is the number of Widom insertions into the configuration of \(N\) molecules. The overall probability \(\alpha_{mn}\) of attempting the insertion with a given position, orientation, and conformation is defined by Eq. (32).
When combined with Eq. (53), Eq. (52) can be further transformed into a single arithmetic average (denoted by \(\langle ... \rangle\) without a subscript) as in Eq. (54), where \(n_{IPC}\) is the same for each N-molecule system configuration \(j\) on which Widom insertions are performed, \(n_{confs}\) is the total number of these system configurations, and \(n_{ins}=n_{IPC} n_{confs}\) is the total number of Widom insertions.
Combining Eqs. (52), (54), (8), and (9) with Eq. (50) yields Eq. (55) for the chemical potential \(\mu\).
The chemical potential \(\mu\) cannot always be calculated in this way for relatively complex molecules,
so the shifted chemical potential \(\mu'\) defined in Eq. (60) is calculated instead
as in Eq. (56), where widom_var is a code variable defined in Eq. (57).
Unlike GCMC insertions, Widom insertions are never accepted and therefore do not have acceptance criteria.
The test molecule is only inserted for the sampling of widom_var and is then always removed.
While the derivation is different for other ensembles, the Widom insertion procedure and
Eqs. (55), (56), and (57) apply to all ensembles
in Cassandra. The identification of code variable names with symbols for widom_insert.f90 is
the same as in Table 11 for move_insert.f90, except for \(\mu'\), which
is only calculated and written to the log file upon completion of the simulation. As described in
Cassandra Output Files, the average widom_var values for each system configuration (step) in which
Widom insertions are performed are written to Widom property files. The final value of \(\mu\)
in kJ/mol for each test particle species in each box is written to the log file after the simulation is completed.
Appendix¶
Inserting a Molecule Randomly¶
To insert a molecule, a position, orientation and molecular conformation must each be selected. The probability of inserting the new molecule at a random location is \(d\mathbf{r}/V\), where \(d\mathbf{r}\) is a Cartesian volume element of a single atom. The probability of choosing the molecule orientation is \(d\mathbf{q}_{rot}/Z_{rot}\), which for a linear molecule is \(d \cos(\theta) d\phi / 4\pi\) and for a nonlinear molecule is \(d \cos(\theta)d\phi d\psi/8\pi^2\). The probability of the molecule conformation only depends on the remaining \(2M-5\) internal bond angles, dihedral angles and improper angles \(\mathbf{q}_{int}\). A thermal ensemble of configurations is Boltzmann distributed \(e^{-\beta U(\mathbf{q}_{int})}/Z_{int}\). The overall probability \(\alpha_{mn}\) is
where we have used Eq. (9) to recover \(Z(1,V,T)\) and recognized that only internal degrees of freedom contribute to the potential energy of the isolated \(N+1\)th molecule in microstate \(n\), \(U(\mathbf{q}_{N+1,n}) = U(\mathbf{q}_{int,N+1,n})\). For a point particle with no rotational or internal degrees of freedom, \(\alpha_{mn}\) reduces to \(d\mathbf{r}/V\). For molecules with internal flexibility, a library of configurations distributed according to \(e^{-\beta U(\mathbf{q}_{int})}/Z_{int}\) can be generated from a single molecule MC simulation. In the reverse move, 1 of the \(N+1\) particles is randomly selected for deletion. The probability \(\alpha_{nm}\) of picking the molecule we just inserted is
The acceptance probability for a random insertion move is
where \(U(\mathbf{q}_{N+1})\) is the intramolecular potential energy of the inserted molecule. \(Q(1,V,T)\) is typically not known a priori, nor is it easily estimated. Substituting Eq. (8) into Eq. (59) and absorbing \(Q_{rot+int}\) into a shifted chemical potential \(\mu'\)
gives the acceptance criteria for inserting a molecule
The terms absorbed into \(\mu'\) are intensive and therefore GCMC simulations using Eq. (61) will converge to a specific average density. However, the value of \(\mu'\) that corresponds to the converged density will not match tabulated values of \(\mu\) computed from experimental data.
Substituting Eq. (19) into Eq. (59) gives
where no terms have been absorbed into the fugacity \(f\). Note also that the partition function has completely been eliminated from the acceptance criteria.
Deleting a Molecule Inserted Randomly¶
The probability \(\alpha_{mn}\) of choosing a molecule to delete is
The probability \(\alpha_{nm}\) of inserting that molecule back in is
The acceptance probability for deleting a molecule inserted randomly is
Note that in \(\Delta U\) is defined differently in Eqs. (61) and (62) than in Eqs. (63) and (64). In the former, the new configuration has more molecules, \(\Delta U = U(\mathbf{q}_n^{N+1}) - U(\mathbf{q}_m^N)\). In the latter, the new configuration has fewer molecules, \(\Delta U = U(\mathbf{q}_n^{N-1}) - U(\mathbf{q}_m^N)\).